Visit the SALMON Bookshop for recommended books on this topic

Behaviour Towards Family & Friends: Kin Selection and Reciprocal Altruism Author Paul Kenyon Overview and Learning Objectives Reflective exercise Altruism - a puzzle for natural selection Hamilton's kin selection theory Kin selection theory in action Recipient's age influences altruism Inheritance of wealth Paternal investment Parent-child conflict Conflict between offspring The 'Wicked stepmother effect' A note on kin selection Trivers' reciprocal altruism theory The prisoner's dilemma Requesting and giving help Cheater-detection is easy, but valid inference is hard Seminar discussion themes References Online resources Points to ponder Heroes and villains Further reading

Enter your search terms Submit search form

Reflective exercise

This lecture considers relationships between people. Before you begin, you may find it useful to focus on who you are related to. This is not an experiment. There are no right / wrong answers. Your responses will not be recorded.

Write the first names of your relatives (if applicable) in the boxes, and then indicate how closely related you perceive yourself to be to this person:

We will return to consider the pattern of your results later.

You may find it useful to view the video 'Tough Choices' from Scientific American Frontiers in which "Princeton researchers study the brain's of test subjects making tough ethical decisions to determine which part of the brain is the seat of morality". Choose the Play video option to jump to demonstrations of two topics  covered in this lecture: Decision making in life and death moral dilemmas and ultimatum games.

Altruism - a puzzle for natural selection

The phrases 'Survival of the fittest' and 'Nature, red in tooth and claw' are associated with Darwin's theory of evolution through natural selection . They portray a world populated by selfish organisms intent on their own survival. This lecture examines the paradox of altruism.

• Why do we co-operate with one another?
• Why do humans and other animals make self-sacrifices that benefit other members of their species?

For example:

• Why do bees sting?
• Why do animals emit alarm calls that reveal their presence to predators?
• Why are some poisonous insects brightly coloured?

These are examples of altruism or self-sacrifice. The existence of altruism posed a significant challenge to Darwin's theory of evolution through natural selection. Recent evidence has highlighted the importance of co-operation to evolution. It turns out that an answer to the altruism-paradox may involve paying more attention to 'selfish genes' rather than selfish people.

Hamilton's kin selection theory

Kin share many common genes. Genes can spread by benefiting other carriers of the same gene. Hamilton proposed the inclusive fitness or kin selection theory to explain altruism or self-sacrifice.

In an altruistic encounter there is:

• an altruist or donor who bears a cost ( c )
• a recipient who gets a benefit ( b )
• a degree of genetic relationship between the donor and recipient

The probability that the altruist and the recipient share a gene is called the coefficient of relatedness ( r ). The diagram shows the extent to which we share genes with our relatives. The value of r varies between 0 and 1. On average we share half of our genes with our brothers, sisters and children ( r=0.5 ), and a quarter of our genes are identical with those of our grandchildren, nephews and nieces ( r=0.25 )

According to Hamilton's Rule altruism pays off if rb>c . In other words, shared genes will profit if the cost to the altruist is less than the benefit to the recipient multiplied by the probability that the recipient shares genes with the donor.

Costs and benefits are expressed in units of fitness or reproductive success with values between 0 and 1.

• A cost of 1 unit of fitness means that the act would reduce the donor's reproductive success by 1 offspring.
• A benefit of 1 unit of fitness means that the recipient would increase their reproductive success by 1 offspring.

For the sake of argument assume you have spare food that you could give to your brother to feed him and his children.

• Assume that the cost to you is 0.1 units of fitness (i.e. if you do this 10 times you will have one less child)
• Assume that the benefit to your brother is 0.25 (i.e. if he receives 4 such donations he will have one more child)

We can test if your altruism would benefit kin selection by putting these values into Hamilton's Rule rb>c where:

• r ( the coefficient of relatedness between you and your brother) = 0.5
• c (the impact on your reproductive success ) = 0.1
• b ( the benefit to your brother's reproductive success) = 0.25
• rb =0.5x0.25=0.125
• c=0.1
• because rb>c (0.125 is greater than 0.1) Hamilton's Rule is satisfied and your altruism would benefit your genes

You might wonder why b and c are not always equal. Why not use the spare food you have to increase your own reproductive success? Well there is a limit to how much you can eat. If you have an abundance of food and your brother is starving, the cost to you of sharing is small, but it may be a matter of life or death to your brother and his children.

Kin selection theory in action

Review your answers to the reflective exercise.

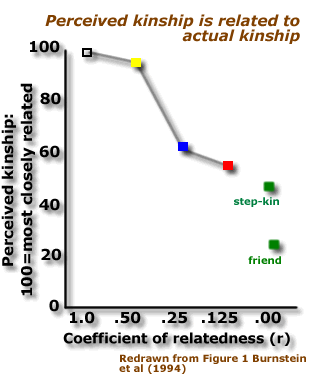
Colour coding was used to break up the table into groups of relatives who are more - or less - related to you.

Does the pattern of your perception of your relatedness to relatives correspond to their actual kinship with you.

You may not have a twin (r = 1.0), but you probably feel more related to

• your mother, father, brother(s) and sister(s) (r = 0.5) than to
• your grandmothers, grandfathers, niece(s) and nephew(s) (r = 0.25) or
• your cousin(s) (r = 0.125) or
• non-relatives (r = 0.00)

Read Study 1: Perceived and Actual Kinship in Burnstein, et al (1994). Journal of Personality and Social Psychology, 67/5, 733-789. Available online

Burnstein et al (1994) and Petrinovich et al (1993) asked people to imagine how they would react in life-and-death situations in which they could prevent the death of a relative. For example imagine that a train is running out of control down a track that branches. You are in charge of the points at a track junction. If the train goes down the left track it will kill one of your relatives. If you send the train down the other track it will kill two strangers. The choice is yours!
	The results reflect what you may have predicted; we are more likely to help a near relative (e.g. brother or sister (r=0.50) than a stranger (r=0.00) in a life-and-death situation.

Recipient's age influences altruism

But what about the age of the relative involved. Would you have predicted that we are less likely to help a younger relative than one who is slightly older? One explanation for our preference for helping young people is that they have higher reproductive value than children or older people. A person's reproductive value is a measure of the probability that they will have children. Older people have lower reproductive value because fertility declines with age. Children have lower reproductive value because they may die before they reach puberty.

Inheritance of wealth

Analysis of bequests (see Cartwright, 2000) made in wills shows that people leave more of their estate:

• to close relatives than distant relatives who have a lower coefficient of relatedness (r)
• to their children than to their siblings (brothers and sisters), even though offspring and siblings have the same coefficient of relatedness (r=0.5) with the deceased. Why do you think this happens?

Paternal investment

According to a simple version of kin selection theory, men should give more resources to their genetic children than to stepchildren. Anderson et al (1999) looked at the odds that a man would give financial support to  'children' who were attending college.   A man's children were classified into one of four types

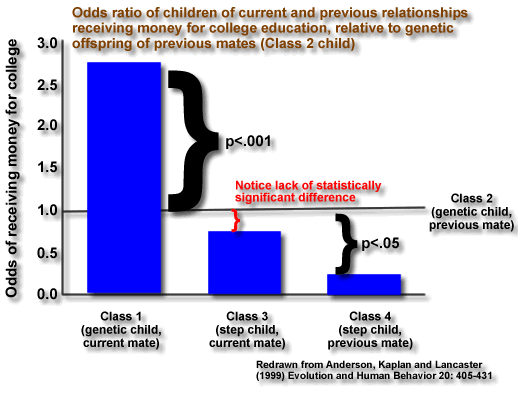Compared to a child fathered by the man, and whose mother was the man's previous partner (Class 2 child), a man is 2.27 times more likely to support a child through college if he was the father of the child and his current partner is the child's mother.  a man is very unlikely to support a child through college if the child's mother was a previous partner, and the man was the child's stepfather Both of these effects are statistically significant. One surprising finding is that a man does not discriminate financially between a child who was born to the man's current partner in a previous relationship (Class 3 child), and a child fathered by the man in a previous relationship (Class 2 child) even though the man is genetically related to the class 2 child, but is only the stepfather of the Class 3 child Men may invest in the children of their current partners in order to convince the current partners that they are 'good providers' and thus persuade their current partner to bear him further children. Men may invest less in their own children from previous relationships because they are not sure that they are the true fathers of the children born whilst they were living with their  previous partners: 'paternity uncertainty'

Parent - child conflict

Trivers applied Hamilton's mathematical formula for kin selection to within-family conflict.  According to Trivers: "Parents are classically assumed to allocate investment in their young in such a way as to maximize the number surviving, while offspring are assumed to be passive vessels into which parents pour the appropriate care. Once one imagines offspring as actors in this interaction, then conflict must be assumed to lie at the heart of sexual reproduction itself-an offspring attempting from the very beginning to maximize its reproductive success would presumably want more investment than its parent is selected to give" (Trivers, 1974).

Here is a section from Buss (1999) which illustrates how conflict can arise from the application of the principles of kin selection.

"Suppose you have one sibling who has the same reproductive value as you. Your mother comes home from a day of gathering with two food items to feed her children. As with many resources, there are diminishing returns associated with each increase in consumption--that is, the value of the first unit of food consumed is higher than the value of the second unit of food. The first unit of food, for example, may prevent starvation, whereas the second unit of food just makes you a little fuller and fatter. Let's say that the first item would raise your reproductive success by four units and the second item of food would raise it an additional three units. Your sibling's consumption of these food items would have the same result, with diminishing returns associated with each added food item.

Now comes the conflict. From your mother's perspective, the ideal allocation would be to give one unit of food to you and one to your sibling. This would net her eight units of increase, four for you and four for your sibling. If either you or your sibling monopolized all the food, however, the gain would only be seven (four for the first item plus three for the second). So from your mother's perspective an equal allocation between her children would yield the best outcome.

From your perspective, however, you are twice as valuable as your sibling--you have 100 percent of your genes, whereas your sibling only has 50 percent of your genes (on average). Therefore, your mother's ideal allocation would benefit you by the four units that you receive plus only two of the units that your sibling receives (since you benefit by only 50 percent of whatever your sibling receives), for a total of six units benefit. If you manage to get all the food, however, you benefit by seven units (four for the first item plus three for the second). Therefore, from your perspective the ideal allocation in this simplified example would be for you to get all the food and your sibling none. This conflicts with your mother's ideal allocation, which is to distribute equally, however. The general conclusion is this: The theory of parent-offspring conflict predicts that each child will generally desire a larger portion of the parents' resources than the parents want to give. Although the above example is simplified in various ways, this general conclusion applies even when siblings differ in their value to the parents and even when the parents have only a single child. If the parents were to go along with the ideal allocation of resources desired by the child, it would take away from other channels through which the parents might be reproductively successful. Interestingly, parent-child conflict over the parent's resources is predicted not merely to occur at particular times such as adolescence, but at each stage of life (Daly & Wilson, 1988).

The theory of parent-offspring conflict yields a number of specific hypotheses that can be tested: (1) parents and children will get into conflict about the time at which the child should be weaned, with the parents generally wanting to wean the child sooner and the child wanting to continue to receive resources longer; (2) parents will encourage children to value their siblings more than children are naturally inclined to value them; and (3) parents will tend to punish conflict between siblings and reward co-operation. " Buss (1999).

This table shows how various allocations of food affect each relative's inclusive fitness

Assume that:

• the mother has two offspring:
• offspring A
• offspring B
• the coefficient of relatedness between the mother and each of her offspring is 0.5
• the coefficient of relatedness between offspring A and offspring B is 0.5
• mother has 2 indivisible units of food to give to her offspring
• eating 1 unit of food would increase an offspring's fitness by 4 units
• eating 2 units of food would increase an offspring's fitness by 7 units i.e. eating more food has diminishing returns

Conflict between offspring

Assume that:

• the mother has two offspring:
• offspring A
• offspring B
• Offspring A and offspring B share the same mother, but have different fathers
• the coefficient of relatedness between the mother and each of her offspring is 0.5
• the coefficient of relatedness between offspring A and offspring B is 0.25
• mother has 2 indivisible units of food to give to her offspring
• eating 1 unit of food would increase an offspring's fitness by 4 units
• eating 2 units of food would increase an offspring's fitness by 7 units i.e. eating more food has diminishing returns

The 'Wicked stepmother effect'

Assume that:

• the mother is caring for two offspring:
• offspring A is her child
• stepchild B is the child of her current partner from a previous relationship
• the coefficient of relatedness between the mother and offspring A is 0.5
• the coefficient of relatedness between mother and stepchild B is 0
• the coefficient of relatedness between offspring A and stepchild B is 0
• mother has 2 indivisible units of food to give to her offspring
• eating 1 unit of food would increase an offspring's fitness by 4 units
• eating 2 units of food would increase an offspring's fitness by 7 units i.e. eating more food has diminishing returns

Trivers' reciprocal altruism theory

Before tackling this section you may find it useful to view

• the video 'Chimps Getting Along' which discusses the possibility that some elements of  morality may be present in chimps
• the video "Keeping the Peace: Studies show both monkeys and apes actively seek to resolve conflicts within their groups, pointing to what scientists believe are the roots of human morality."

Trivers (1971) has suggested another theory of why we co-operate with people who are not necessarily related to us. This works on the principle of " if you scratch my back, I'll scratch yours" This theory depends on important preconditions:

• costs should be small compared to benefits
• the recipient should be able to recognize the donor
• the donor and recipient should regularly exchange roles

The prisoner's dilemma

The prisoner's dilemma game is a way of studying how people behave in a situation with different rewards for co-operating with, and cheating on, another person. For the purposes of this game you are asked to imagine that you and a colleague have committed a crime. You enter into a pact with your colleague-in-crime in which you both agree to say nothing to the police if you are interviewed. Subsequently the police interview both of you in separate rooms. They offer you a 'deal'. They have enough evidence to charge you both with a relatively minor crime for which you will both serve one year in prison. If you both confess to the major crime, you will each receive a five year sentence for co-operating with the authorities. But here's the twist! If you confess and your colleague does not confess, he will receive a ten year sentence and you will not be prosecuted. Likewise if you keep quiet about the major crime, but your friend confesses, you will serve ten years in prison and he will walk free. The choice is yours!. Here are your options:

As you can appreciate there is a great temptation to confess and thereby cheat on your earlier agreement with your colleague. If you were to play the prisoner's dilemma only once this might be your preferred strategy, but what happens if you had to face the same situation again. This variation of the game is called the iterated prisoner's dilemma . In this variation of the game you may be punished by your colleague on the next round of the game.

There is a great deal of interest in the prisoner's dilemma game because it is a model for real-world situations in which people and animals co-operate and compete with each other. For example the proliferation of nuclear arms during the Cold War can be analysed in terms of prisoner's dilemma strategies. Likewise the problem of persuading people to accept the inconvenience associated with abandoning private cars in favour of public transport, or separating their domestic rubbish for recycling are variations on the theme of the 'tragedy of the commons'.

What is the best strategy to adopt in the iterated prisoner's dilemma game. There are various possibilities:

• always co-operate - the 'dove' or meek and mild strategy
• always cheat - the 'hawk' strategy
• always retaliate - the tit for tat strategy
• cheat on every third game
• co-operate unless your colleague cheats twice in a row
• etc.

It doesn't take much imagination to realize that finding the best strategy would be very important for foreign policy advisers to leaders of world superpowers.

It turns out a good strategy is to play tit for tat :

• co-operate on the first game
• never be the first to cheat
• retaliate on the next game if the other player cheats, then co-operate if the other player responds by co-operation

Soldiers in trenches on the Western front in World War 1 engaged in tit for tat shooting. The commanding generals stamped out this behaviour by court-martialling some soldiers.

Picture: "Humanity - Stretcher-bearer Post, 9th Field Ambulance" by Gilbert Rogers (Official War Artist). From Swedish University Network SUNET Archive ftp.sunet.se

But tit for tat can run into problems if you make an error . For example you might loose concentration, and imagine that the other player has cheated when in fact they made a co-operative move. A slight modification of the strategy overcomes this problem - only retaliate if the other player cheats twice in a row - the generous tit for tat strategy. Cartwright (2000) provides a clear explanation of the effectiveness of these strategies and variations such as the Pavlov 'win stay, lose shift' strategy.

Requesting and giving help

Gaulin & McBurney (2001) review the conditions that encourage us to ask for, and give help.

We are more likely to give assistance if:

• the cost is low
• the need is urgent
• the person we help will be able to help us in future i.e. they can reciprocate our behaviour
• our reputation is at stake or our behaviour will be observed by others

We are more likely to ask for help if:

• we feel we will be in a position to reciprocate the helper in the future

Ultimatum games indicate that people are more altruistic than mathematical game theory would predict.

Imagine I have £10 which you can split with someone else. If the other player accepts the split then you each get the amount you specified. If your offer is rejected, then you both get nothing. How much would you offer to share?

Game theory predicts that the best strategy is for you to offer £1 and keep £9 for yourself. But the majority of people offer the other player £5 and keep £5 for themselves.

Maybe you are worried that you will be punished for being mean. The other player might reject £1 in order to punish your selfishness.

Would you change your offer if the rules of the game are changed so that the other player cannot reject your offer?

This manipulation does have an impact on what people offer, but only 20% of subjects give away £1 and keep the remaining £9. And more than 20% of players split the money equally with the other player.

One explanation for people's niceness in ultimatum games is that they feel their reputation would be damaged if they behaved selfishly. However even under 'double-blind' conditions - in which anonymity is preserved - some people still fail to act selfishly.

Cheater-detection is easy, but valid inference is hard

Do you know who these men are, and why they are famous? Humans are exquisitely sensitive to cheating . We scan our environment to detect people who cheat. We remember the faces of people who have been introduced as cheaters more effectively than pictures of non-cheaters we dislike 'free-riders' we are interested in gossip about the exploits (often sexual) of people we know we take steps to preserve our reputations (Gaulin & McBurney, 2001) we feel guilt after cheating or failing to reciprocate a kindness

If you are a student at the University of Plymouth you may be familiar with the following logical problem:

You have been hired as a clerk. Your job is to make sure that a set of documents is marked correctly according to the following rule:

If the document has a D rating, then it must be marked code 3

You have been told that there are some errors in the coding of the documents, and that you need to find the errors. Each document has a letter rating on one side and a numerical code on the other. Here are four documents. Which document(s) do you need to turn over to check for errors?

Here is another problem: You have been hired as a bouncer in a bar and you must enforce the following rule:

If a person is drinking beer, then they must be over twenty years old.

The cards below have information about four people at the bar. One side of each card lists a person's age and the other side shows what they are drinking. Which card(s) do you need to turn over to be sure no one is breaking the law?

The bouncer's problem is easier to solve.

• turn over the 'beer' card to make sure the person is over twenty,
• turn over the '16 years' card to ensure the person is not drinking beer.

But the clerk's document checking problem is more difficult.

• turn over the 'D' card to make sure it is marked 3.
• the card marked '7' must be turned over to ensure it does not have a 'D' on the other side.

About 75% of students solve the bouncer's task but less than 25% get the clerical task correct. Don't worry if you are not one of the 25%. I didn't get it right first time and even now I can't solve that type of logical problems. But I can detect a 'cheater' at 20 paces!

It turns out that both tasks have exactly the same logical structure.

Confused by the logic behind the clerk problem? I still am , and I'm writing this stuff. It turns out that you can solve the problem if you have been taught the rules of valid inference as part of a course on logic. These problems are examples of the Wason selection task . I get the impression that people who have been taught logic have spent years trying to figure out why the rest of us can't get our heads around the clerk problem. It seems that the majority of us can solve Wason's selection tasks if they involves cheater detection -e.g. the bouncer problem. Cosmides and Tooby suggest that have evolved a mental ability to spot cheaters in order to be able to engage in reciprocal altruism . The rules of logical inference are important to scientists because they need to check hypotheses for examples that would falsify them. The rest of us need to be equipped with the mental capacity to spot a rogue car dealer before we drive of in a gleaming 'death-trap'. Can you pick out 'Nasty Nick' who cheated on the TV show 'Big Brother' and Caroline who replaced him from these pictures of contestants?

References

• Anderson, Kaplan and Lancaster (1999) Paternal Care by Genetic Fathers and Stepfathers I: Reports from Albuquerque Men. Evolution and Human Behavior 20: 405–431. Available online
• Burnstein, Crandall and Kitayama (1994). Some Neo-Darwinian Decision Rules for Altruism Weighing Cues for Inclusive Fitness as a Function of the Biological Importance of the Decision. Journal of Personality and Social Psychology, 67/5, 733-789. Available online
• Buss (1999). Evolutionary Psychology: The New Science of the Mind,Allyn & Bacon, Boston. Section available online
• Burnstein et al, (1994). Journal of Personality and Social Psychology , 67, 1994
• Cartwright, (2000). Evolution and Human Behaviour, Macmillan Press, Basingstoke, 2000
• Gaulin & McBurney, (2001). Psychology: An Evolutionary Approach , Prentice Hall, New Jersey, 2001
• Petrinovich et al, (1993). Journal of Personality and Social Psychology , 64, 467-478, 1993
• Trivers (1971). Quarterly Review of Biology , 46, 35-57, 1971
• Trivers (1974). 1974. Parent-offspring conflict. American Zoologist 14: 249-264
  

Online resources

• Anderson, Kaplan and Lancaster (1999) Paternal Care by Genetic Fathers and Stepfathers I: Reports from Albuquerque Men. Evolution and Human Behavior 20: 405–431. Available online
• Burnstein, Crandall and Kitayama (1994). Some Neo-Darwinian Decision Rules for Altruism Weighing Cues for Inclusive Fitness as a Function of the Biological Importance of the Decision. Journal of Personality and Social Psychology, 67/5, 733-789. Available online
• Buss (1999). Evolutionary Psychology: The New Science of the Mind,Allyn & Bacon, Boston. Section available online
• Caporael (2001). Evolutionary Psychology: Toward a Unifying Theory and a Hybrid Science. Annual Review of Psychology 2001, available online
• Daly and Wilson (1996). Evolutionary Psychology and Marital Conflict: The Relevance of Stepchildren. In D.M. Buss & N. Malamuth (Eds.), Sex, power, conflict: feminist and evolutionary perspectives. New York: Oxford University Press, pp 9-28. Available online
• Daly and  Wilson. (1998). The Truth About Cinderella. New Haven: Yale University Press. Excerpts available online
• Kolliker and Richner (2001) Parent–offspring conflict and the genetics of offspring solicitation and parental response. Animal Behaviour , 2001, 62, 395–407. Available online
• Stone, Cosmides, Tooby, Kroll, and Knight (2002) Selective Impairment of Reasoning About Social Exchange in a Patient with Bilateral Limbic System Damage. Proceedings of the National Academy of Sciences, August 13, 2002
• Scientific American Frontiers (1992)   "The Power of Persuasion" video available here
• Scientific American Frontiers (1995). "Keeping the Peace: Studies show both monkeys and apes actively seek to resolve conflicts within their groups, pointing to what scientists believe are the roots of human morality." video available online
• Scientific American Frontiers (1995). "Chimps Getting Along:Observations by primatologist Frans de Waal suggest chimps live by the Golden Rule." video available online
• Scientific American Frontiers (1999). "Masked Killers. Stronger Masked Booby chicks kill their smaller siblings to better ensure their own survival, and that of their mothers as well." video available online
• Scientific American Frontiers (2002). "Tough Choices: Princeton researchers study the brain's of test subjects making tough ethical decisions to determine which part of the brain is the seat of morality". video available online
• Sugiyama,  Tooby, and  Cosmides (2002). Cross-Cultural Evidence of Cognitive Adaptations for Social Exchange among the Shiwiar of Ecuadorian Amazonia. Proceedings of the National Academy of Sciences, August 13, 2002
• Sugiyama (2002) describes  the background to this work, a summary of the main  findings, and a discussion of the implications.

Points to ponder

Here are some jaundiced views of human ethics / morals.

• 'Ethics is an illusion fobbed on us by our genes to get us to co-operate'
• 'Our belief in morality is merely an adaptation put in place to further our reproductive ends'
• 'Morality is a means whereby individual human beings attempt to induce altruism in others in their own self interest'

But maybe something of the human spirit is missing in these cogitations ...

Heroes and villains

Here are some people made famous by outstanding acts of altruism and cheating.

'I am just going outside, and may be away some time'

In the early years of the last century, a party of explorers led by Captain Scott set sail for the Antartic. In Scott's words "The main object of this expedition is to reach the South Pole, to secure for the British Empire the honour of this achievement."

On 17 January 1911, Scott's expedition reached the Pole; he wrote: "Great God! this is an awful place and terrible enough for us to have laboured to it without the reward of priority". Their disappointment was due to a Norwegian team having beaten them to the Pole.

The journey back to base was a nightmare. On the 17 February 1912 one of the expedition members, (Evans) died at the foot of the Beardmore Glacier after several bad falls.

The others struggled on, getting weaker and frost-bitten, especially Oates who, at the end of another month could go no further and knew he was holding back his companions. Scott wrote: "We knew the end had come. One morning he said, 'I am just going outside and may be some time'. He went out (of the tent) and we have not seen him since".

Scott, Wilson and Bowers knew that Oates was going out to die for their sakes. Scott wrote: "Though we tried to dissuade him, we knew it was the act of a brave man and an English gentleman. We all hope to meet the end with a similar spirit."

Down in the South where the blizzards blow,
Four men struggled along in the snow.
Bowers and Wilson and Captain Scott,
They could walk, but Oates could not.
Slower and slower, day by day,
They dragged the sled on which he lay.
Each man thought, though none would say,
But for Oates we might get away.....

'Never before have so many owed so much to so few'

The Battle of Britain was a crucial moment in World War II. Although short of planes and pilots, the Royal Air Force held off the Luftwaffe and prevented a German invasion. Churchill called it Britain's "Finest Hour".

.... and villains

The star Canadian sprinter Ben Johnson received a lifetime ban for steroid use after running 100 meters in 9.79 seconds at the Seoul Olympics.